数据结构-6
树和二叉树
树的概念
- 树:一个有限集,可以为空,非空时有且只有一个根结点,其余结点可以分为多个不相交的有限集(子树)
- 结点的度:结点的子树个数
- 树的度:树的所有结点中最大的度数
- 叶子结点:度为0的结点
- 父结点:有子树的结点是其子树的根节点的父结点
- 子结点/孩子结点:若A结点是B结点的父结点,则称B结点是A结点的子结点
- 兄弟结点:具有同一个父结点的各结点彼此是兄弟结点
- 路径和路径长度:从结点n1到nk的路径为一个结点序列n1,n2,…,nk。ni是ni+1的父结点。路径所包含边的个数为路径的长度
- 祖先结点:沿树根到某一结点路径上的所有结点都是这个结点的祖先结点
- 子孙结点:某一结点的子树中的所有结点是这个结点的子孙
- 结点的层次:规定根结点在1层,其他任一结点的层数是其父结点的层数加1
- 树的深度:树中所有结点中的最大层次是这棵树的深度
二叉树
二叉树概念
二叉树:一个有穷的结点集合。这个集合可以为空;若不为空,则它是由根结点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。二叉树的子树有左右顺序之分。
二叉树的五种基本形态:
斜二叉树:只有左子节点或只有右子节点的二叉树,度为1,只有左子节点或右子节点
满二叉树/ 完美二叉树:除最后一层无任何子结点外,每一层上的所有结点都有两个子结点的二叉树
完全二叉树:有n个结点的二叉树,对树中结点从上至下、从左到右顺序进行编号,编号为i(1≤i≤n)结点与满二叉树中编号为i结点在二叉树中的位置相同(能和满二叉树完全重叠,编号相同)
按从上至下、从左到右顺序存储n个结点的完全二叉树的结点父子关系:(顺序存储)
- 根结点的序号为1
- 非根结点(序号i>1)的父结点的序号是:i / 2
- 结点(序号为i)的左孩子结点的序号是:2 * i,若2*i > n,则没有左孩子
- 结点(序号为i)的右孩子结点的序号是:2 * i + 1,若2*i+1 > n,则没有右孩子
普遍规律:
一个二叉树第i层的最大结点数为:2i-1,i≥1
深度为k的二叉树有最大结点总数为:2k-1,k≥1
对任何非空二叉树T,叶结点个数为n0,度为1的结点个数为n1,度为2的结点个数为n2,则二叉树的总边数:N=2*n2+n1,总结点数:N′=n0+n1+n2,总叶子结点数:n0=n2+1
二叉树的三种遍历:
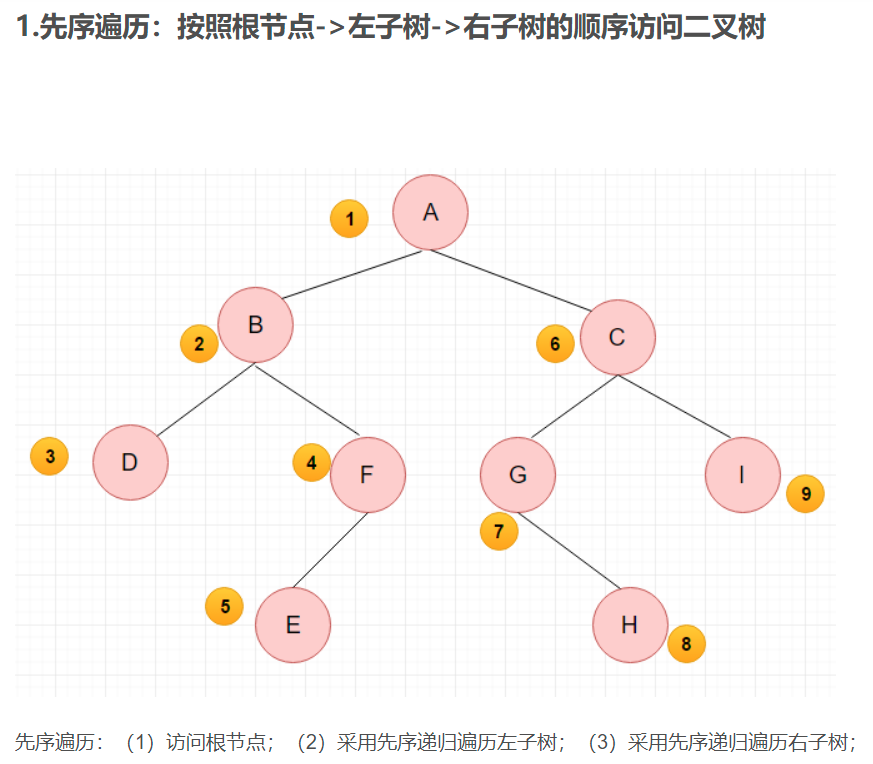
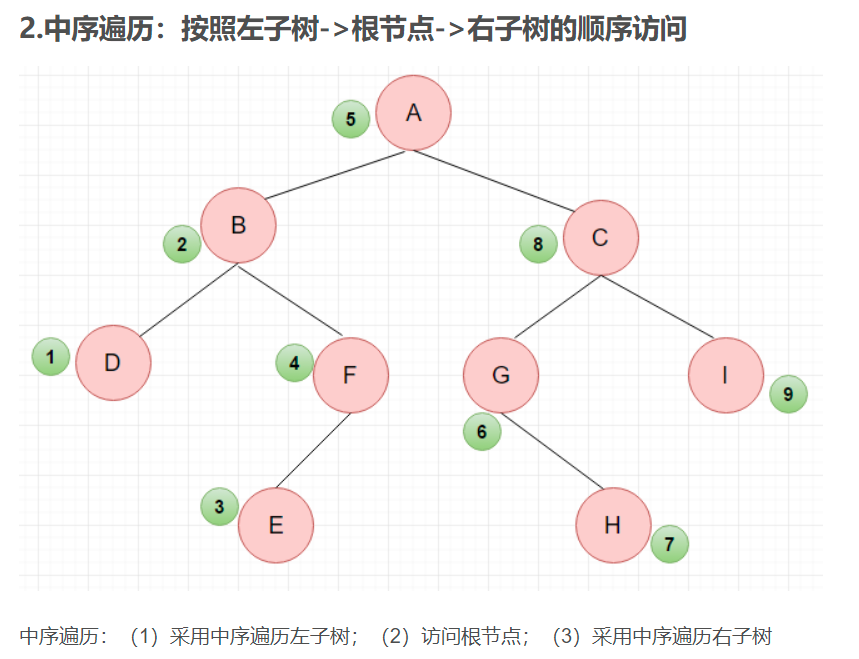
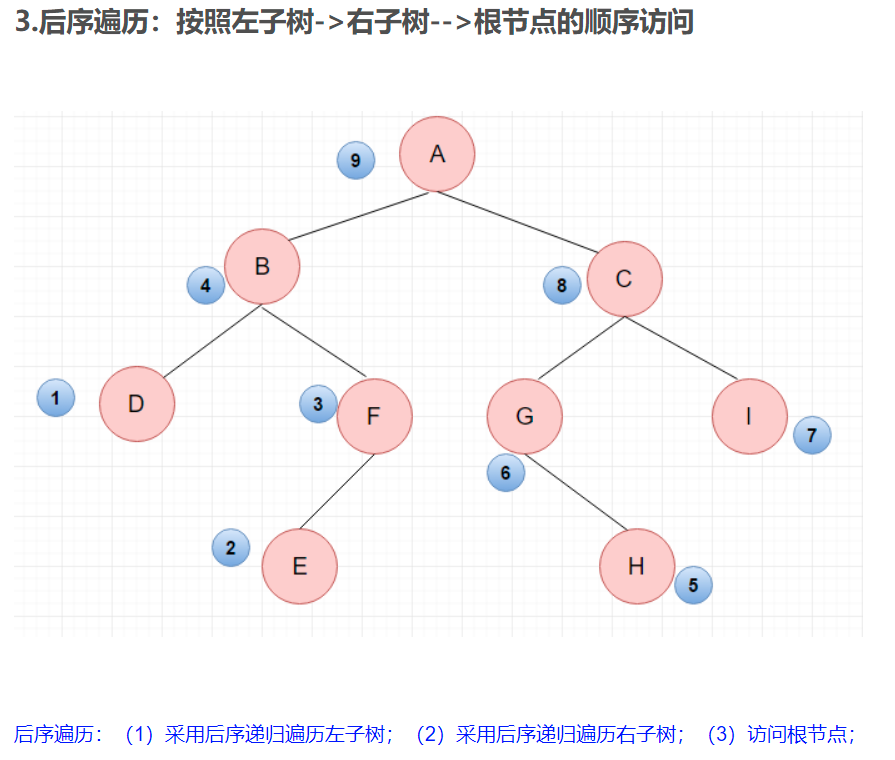
二叉树操作
创建/初始化
由于树的顺序表结构分配的空间通常只适用于完全二叉树,会造成普通二叉树的空间浪费,所以二叉树一般使用链式结构存储
typedef struct BTnode{ |
由于二叉树用递归算法较快,涉及到的先序、中序、后序三种输入方式时,只需要调整根节点的输入顺序即可
void Create(BTree &T) //传入要操作的结点T |
遍历
在创建的时候,相当于也就遍历了一次二叉树,故而除却赋值之外的结构都十分相似,而且由于二叉树已经建立,可以通过二叉树的结点指针是否为空判断遍历是否结束
void Traverse(BTree T) //传入需要往下位置遍历的根节点 |
计算深度
二叉树深度为左右子树中深度较大者加1,故而需要递归求取左右子树的深度,再比较后加1
int depth(BTree T) //传入需要往下求取深度的根节点 |
线索二叉树
创建
线索二叉树将二叉树中空置的左右指针域利用起来,存储沿某种顺序遍历二叉树后继结点的地址,比二叉树多设置左右标志,当标志为1(true)时,表示有对应的子节点(左标志为1,左指针域存储左孩子的地址),否则对应指针域则存储某种顺序遍历二叉树时的下一个结点的地址
其中,左指针域为线索时,指向前驱,右指针域为线索时指向后继
typedef struct DBTnode |
二叉树中序线索化
DBTnode *p; //p为全局变量,是指向线索二叉树结点的指针 |
遍历中序线索二叉树(非递归)
void OTraverse(DBTree T) |





