数据结构-5
串类型
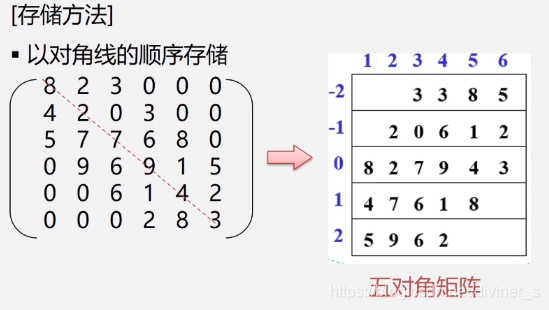
存储结构
串的存储结构可以使用顺序和链式结构,顺序结构中又分为定长和堆式存储结构,但由于链式不如顺序结构灵活,操作简单,故而此处只写入顺序结构
顺序-定长存储
typedef struct{ |
顺序-堆式存储
typedef struct{ |
模式匹配算法
串的模式匹配用于在主串中寻找子串,如果匹配成功,则确定相匹配的子串中第一个字符在主串s中出现的位置
BF算法
int Index_BF(Sstring s,Sstring t,int pos) |
KMP算法
int Index_KMP(Sstring s,Sstring t,int pos) |
数组
二维数组的顺序存储
已知一维数组中a【i】的存储位置在a+i处,二维数组因主序不同分为两种存储结构(常用行序)
设每个数据元素占L个存储单元,则二维数组A[0…m-1,0…n-1](下标从0开始,共有m行n列)中任一元素a【i】【j】的存储位置如下:
行为主序的存储结构:
$$
LOC(i , j) = LOC(0 , 0) + (n * i + j) L
$$
列为主序的存储结构:
$$
LOC(i , j) = LOC(0 , 0) + (m * j + i) L
$$
其中,LOC(i,j)是a【i】【j】的存储位置
LOC(0,0)是a【0】【0】的存储位置,即二维数组A的起始存储位置、也称为基地址或基址
故而总结可知:
$$
LOC(i , j) = 基址 + (副序长度 * 主序标号 + 另一标号) * 数据所占存储单元
$$
特殊矩阵的压缩存储
对称矩阵
特点:在n*n的矩阵a中,1<= i,j <= n
存储方法:只存储下(或者上)三角(包括主对角线)的数据元素。共占用n(n+1)/2个元素空间。
上下三角中的元素均为:n(n+1) / 2
可以以行序为主序将元素存放在一个一维数组a[n(n+1) / 2]中,a[k]的位置可如下公式确定
$$
k=主序序号(主序序号-1)/2+副序序号-1,主序>=副序
$$
注:上式的k从0开始计算
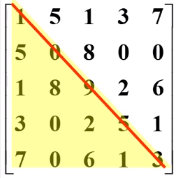
三角矩阵

对角矩阵

稀疏矩阵

广义表
一般记作LS(a1,a2,……,an),其中LS为广义表的名称,n为广义表的长度,其中的元素可以是单个数据(原子)也可以是广义表(子表),一般小写为原子,大写为子表
广义表示例:
- A=()——空表,长度为0
- B=(e)——只有一个原子,为e,长度为1
- C=(a,(b,c,d))——有一个原子a和一个子表(b,c,d),共两个元素,长度为2
- D=(A,B,C)——有三个子表,即三个元素,长度为3
- E=(a,E)——一个递归的表,长度为2
注:广义表A=(())和广义表B=()是不相同的,A为有一个空子表,长度为1的广义表,而B是一个空表,长度为0